Explore by Topic
Stay Connected
Don't miss out on the latest technology delivered to your email every 2 weeks. Sign up for the DSDE newsletter.
The TWA Editorial Board is accepting nominations for “TWA Energy Influencers 2024: Young Professionals Who Energize Our Industry.” Nominate a YP by 1 June 2024.
SPE President Terry Palisch is joined by Paige McCown, SPE senior manager of communication and energy education, to discuss how members can improve the industry’s public image.
From the first supercomputer to generative AI, JPT has followed the advancement of digital technology in the petroleum industry. As the steady march of innovation continues, four experts give their views on the state and future of data science in the industry.
-
Jim Gable, president of Chevron Technology Ventures, shares how CTV works with startups and how their technologies go big.
-
A total of 15 companies, including five small businesses, were recognized this year for their demonstrated advancements in the industry.
-
More than two dozen artificial intelligence systems are being celebrated for delivering massive value to the national oil company.
-
Supervised learning was used to develop an ensemble of models that account for historical production data, geolocation parameters, and completion parameters to forecast production behavior of oil and gas wells.
-
This paper develops a deep-learning work flow that can predict the changes in carbon dioxide mineralization over time and space in saline aquifers, offering a more-efficient approach compared with traditional physics-based simulations.
-
The authors of this paper propose a hybrid approach that combines physics with data-driven approaches for efficient and accurate forecasting of the performance of unconventional wells under codevelopment.
-
This work provides a new modeling tool, validated against a static-wellbore solver and field data, to estimate and manage downhole temperature in higher-temperature oil, gas, and geothermal wells.
-
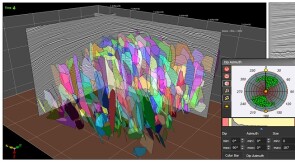
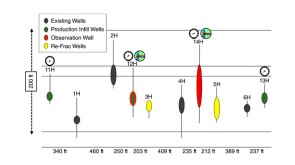
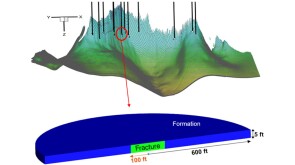
This paper’s focus is a case study of an Eagle Ford refracturing project in which a range of completion designs were trialed with an approach using offset sealed wellbore pressure monitoring and fiber-optic strain.
-
This paper describes a full-field and near-wellbore poromechanics coupling scheme used to model productivity-index degradation against time.
-
The authors integrated azimuths and intensities recorded by fiber optics and compared them with post-flowback production-allocation and interference testing to identify areas of conductive fractures and offset-well communication.
-
This paper addresses the challenges related to well control and the successful implementation of deep-transient-test operations in an offshore well in Southeast Asia carried out with the help of a dynamic well-control-simulation platform.
-
If optimized to scale, fast fission reactors could play a role in reducing emissions in field operations by producing carbon-free electricity.
-
This paper describes how near-real-time tracer data from the onsite tracer analysis enabled the operator of the Nova field to interactively optimize two well cleanups.
-
Slickline-Deployed Fiber-Optic Cable Provides First Production Profile for High-Temperature Gas WellThis paper describes a case study in which, in the absence of a conventional production log, distributed fiber-optic sensing, in conjunction with shut-in temperature measurements, provided a viable method to derive inflow zonal distribution.