Trending Content
The inaugural SPE Workshop on CCUS Management in China was held in April in Qingdao. The workshop highlighted recent advances and technical challenges in CCUS management and attracted 104 attendees representing 19 organizations from eight countries.
The Norwegian oil company said it may spend more than $130 million to get in on the emerging lithium brine business in Texas and Arkansas.
The agreement puts an early contractual framework in place for closer collaboration sooner on the project pair.
-
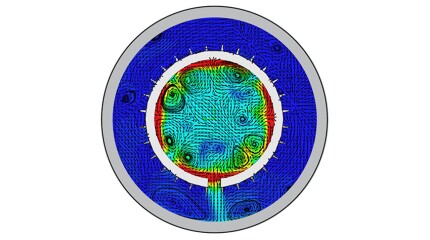
Traditional oil extraction methods hit a snag in noncontiguous fields, where conventional flow-based EOR techniques falter. In southwest Texas, a producer faced imminent shutdown of its canyon sand field due to rapid production decline. Field tests using elastic-wave EOR determined whether the field could be revitalized or if a costly shut-in process was inevitable.
-
The health, safety, and environment (HSE) discipline is one of the broadest in SPE, from the perspectives of both its scope and its cross-discipline impact. As JPT celebrates 75 years, former HSE Technical Director Roland Moreau examines some of the defining moments in the history of HSE in the industry, the growth of the discipline, and the challenges it still faces.
-
Losing drill-hungry independent and private companies in the region to robust M&A will mean an activity slowdown that is expected to impact volumes coming from the nation’s largest oil field.
Get JPT articles in your LinkedIn feed and stay current with oil and gas news and technology.
-
A 44-well development tests what ConocoPhillips has learned about maximizing the value of the wells by figuring out how they drain the reservoir.
-
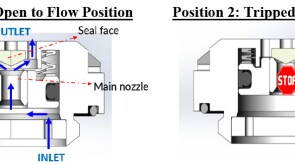
To avoid costly interventions like sidetracking or wellbore abandonment, a check-valve system was installed near the sandface within three injector wells which prevented the mobilization of fines from the reservoir into the wellbore by stopping backflow.
-
The challenges that geothermal energy faces to become a leading player in the net-zero world are well within the areas of expertise of the SPE community, ranging from rapid technology implementation and learning-by-doing to assure competitiveness to establishing suitable funding mechanisms to secure access to capital.
-
The Mexican state oil company turns to the bit in a bid to add meaningful reserves from the deep Mexican Gulf.
Access to JPT Digital/PDF/Issue
Sign Up for JPT Newsletters
Sign up for the JPT weekly newsletter.
Sign up for the JPT Unconventional Insights monthly newsletter.
President's Column
-
SPE President Terry Palisch is joined by Jennifer Miskimins, department head of petroleum engineering at the Colorado School of Mines, to discuss the academic aspect of petroleum engineering and its future.
-
SponsoredThe oil and gas industry makes up 40% of all anthropogenic methane emissions because of leaks at the wellsite. Fortunately, the well pad is often where methane emissions are easiest to address through a mitigation strategy of optimized maintenance and process control—all enabled by instrumentation insight.
-
SponsoredExpanding its portfolio of high-tier technologies, TAQA develops a high-performance perforation-plugging patented product.
-
SponsoredWith almost three-quarters of the global greenhouse gas emissions coming from the energy sector, there is a heavy burden and a huge responsibility on the shoulders of all countries of the world to transform the energy sector to be cleaner and greener by eliminating these emissions.
-
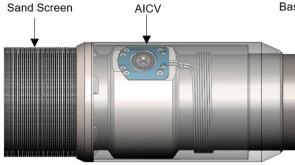
SponsoredSmart completions using autonomous outflow control devices significantly helped in improving reservoir management and increasing oil and gas field productivity by enhancing the injection wells' performance.
Technology Focus
Recommended for You (Login Required for Personalization)
-
Texas has become an early hot spot for geothermal energy exploration as scores of former oil industry workers and executives are taking their knowledge to a new energy source.
-
The developer of the recently emerged anchorbit technology is preparing to drill its first geothermal well next year in Germany.
-
Ignis H2 Energy and Imeco Inter Sarana announced a strategic partnership to expedite geothermal development in Indonesia.
Content by Discipline