Trending Content
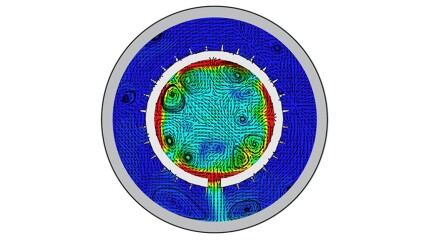
Operators are turning the tide on the Lower Tertiary trend with increasingly large stimulations that are also pushing the limits of offshore technology.
The prestigious award celebrates OTC exhibitors who are revolutionizing the industry with their groundbreaking technologies. This year, 15 exceptional technologies—five of which hail from small businesses—were chosen for their advancements. Join us in recognizing these trailblazers who are shaping the future of offshore energy.
The health, safety, and environment (HSE) discipline is one of the broadest in SPE, from the perspectives of both its scope and its cross-discipline impact. As JPT celebrates 75 years, former HSE Technical Director Roland Moreau examines some of the defining moments in the history of HSE in the industry, the growth of the discipline, and the challenges it still faces.
-
Matthew Bryant has spent years trying to convince engineers that the API proppant testing standard has significant limitations. And he may well be right.
-
At COP28, more than 50 oil and gas companies took a historic step toward decarbonization by launching the Oil & Gas Decarbonization Charter. This article explores the importance of this effort, the opportunities available to the industry to reduce its Scope 1 and 2 emissions, and the key technologies needed to achieve the net-zero goal.
-
Losing drill-hungry independent and private companies in the region to robust M&A will mean an activity slowdown that is expected to impact volumes coming from the nation’s largest oil field.
Get JPT articles in your LinkedIn feed and stay current with oil and gas news and technology.
-
Traditional oil extraction methods hit a snag in noncontiguous fields, where conventional flow-based EOR techniques falter. In southwest Texas, a producer faced imminent shutdown of its canyon sand field due to rapid production decline. Field tests using elastic-wave EOR determined whether the field could be revitalized or if a costly shut-in process was inevitable.
-
A 44-well development tests what ConocoPhillips has learned about maximizing the value of the wells by figuring out how they drain the reservoir.
-
Jennifer L. Miskimins is the nominee for 2026 SPE President. She and six others make up the new slate of nominees recommended for positions open on the SPE International Board of Directors.
-
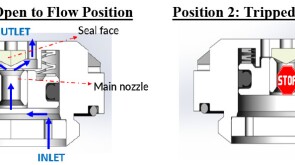
To avoid costly interventions like sidetracking or wellbore abandonment, a check-valve system was installed near the sandface within three injector wells which prevented the mobilization of fines from the reservoir into the wellbore by stopping backflow.
Access to JPT Digital/PDF/Issue
Sign Up for JPT Newsletters
Sign up for the JPT weekly newsletter.
Sign up for the JPT Unconventional Insights monthly newsletter.
President's Column
-
SPE President Terry Palisch is joined by Jennifer Miskimins, department head of petroleum engineering at the Colorado School of Mines, to discuss the academic aspect of petroleum engineering and its future.
-
SponsoredExpanding its portfolio of high-tier technologies, TAQA develops a high-performance perforation-plugging patented product.
-
SponsoredWith almost three-quarters of the global greenhouse gas emissions coming from the energy sector, there is a heavy burden and a huge responsibility on the shoulders of all countries of the world to transform the energy sector to be cleaner and greener by eliminating these emissions.
-
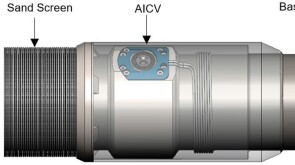
SponsoredSmart completions using autonomous outflow control devices significantly helped in improving reservoir management and increasing oil and gas field productivity by enhancing the injection wells' performance.
-
SponsoredWith more surface facilities and infrastructure in oil and gas fields, well casing integrity is becoming an even bigger challenge. This article sheds light on the optimum way to deal with the increasing casing integrity challenges in the Middle East through field monitoring and time-lapse casing-integrity and corrosion-inspection logging.
Technology Focus
Recommended for You (Login Required for Personalization)
-
Texas has become an early hot spot for geothermal energy exploration as scores of former oil industry workers and executives are taking their knowledge to a new energy source.
-
The developer of the recently emerged anchorbit technology is preparing to drill its first geothermal well next year in Germany.
-
Ignis H2 Energy and Imeco Inter Sarana announced a strategic partnership to expedite geothermal development in Indonesia.
Content by Discipline