TWA Energy Influencers 2024: Nominations Open
The TWA Editorial Board is accepting nominations for “TWA Energy Influencers 2024: Young Professionals Who Energize Our Industry.” Nominate a YP by 1 June 2024.
Read more...
Trending Content
The energy transition, one of the main topics of the decade, deals with the possibility of producing clean energy while minimizing the impact on people’s behavior. However, one indicator of the amount of energy we use is revealed by the number of lights turned on at night.
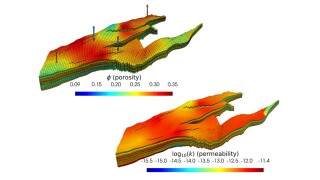
In the final part of this three-part series, we extend our learning of Part 2 to the multivariate model and train a single model to predict three outcomes: oil, gas, and water.
This one-day event will be held 8 May during the 2024 Offshore Technology Conference in Houston.
-
Connect with industry experts, explore careers in the exciting world of oil, gas, and energy, and get the resources you need for a bright career. The future of energy is calling—are you ready to answer?
-
Workers across the Bakken Shale have begun receiving help from displaced Ukrainians as part of the US federal government’s ‘Uniting for Ukraine’ program.
-
Learn how to prepare the perfect CV and download examples to help guide you in your job search.
-
In Part 1 of this three-part series, we use long short-term memory (LSTM), a machine learning technique, to predict oil, gas, and water production using real field data.
-
Explore the history of Howard Hughes Sr., inventor of the two-cone roller bit, in Part 1 of this two-part series highlighting the Hughes family legacy in the oil and gas industry.
-
Explore the challenges associated with fiber-optics data analysis and how recent advances in technology can be leveraged to maximize the value of the data.
-
These seven open-source simulators are available for free use and are among the best available in the industry.
-
Dan Jeavons, Shell’s VP of computational science and digital innovation, discussed the findings in MIT’s recent report on digital technology’s impact on a net-zero emissions future with Aman Srivastava, TWA deputy editor in chief.
Stay Connected
Get the latest articles on career development topics to your inbox. Sign up for the TWA monthly newsletter.
-
This photo was taken in March 2023, during my first period on a platform rig, it is a dream come true. Nine years ago, I discovered drilling, which showed me a new world with amazing postcards. I’m in workover jobs as a petroleum engineer in Mexico. I sent this picture to my brother to share my enormous happiness to be here.
-
Thirty three years in the oil and gas industry and I never get tired of watching a sunset. This photo was taken from the helideck of the Ocean Onyx mobile offshore drilling unit which is currently drilling for Beach Energy, offshore Australia. I’m looking out over the Otway Basin and the vast expanse of the Southern Ocean. How far south are we? Well if I was to get in…
-
I’m proud to share the nice celebration of a big milestone recently achieved: 100,000 b/d produced in Iara license by the floating, production, storage and offloading (FPSO) vessel P-68. Congratulations to Total E&P Do Brasil and all involved. It is only the beginning of this incredible adventure.